Causality in branching time series
Theoretical Systems Biology Retreat
(German Cancer Resarch Center, Heidelberg)
Ellwangen · 22 June 2016

Gene expression data for branching lineages
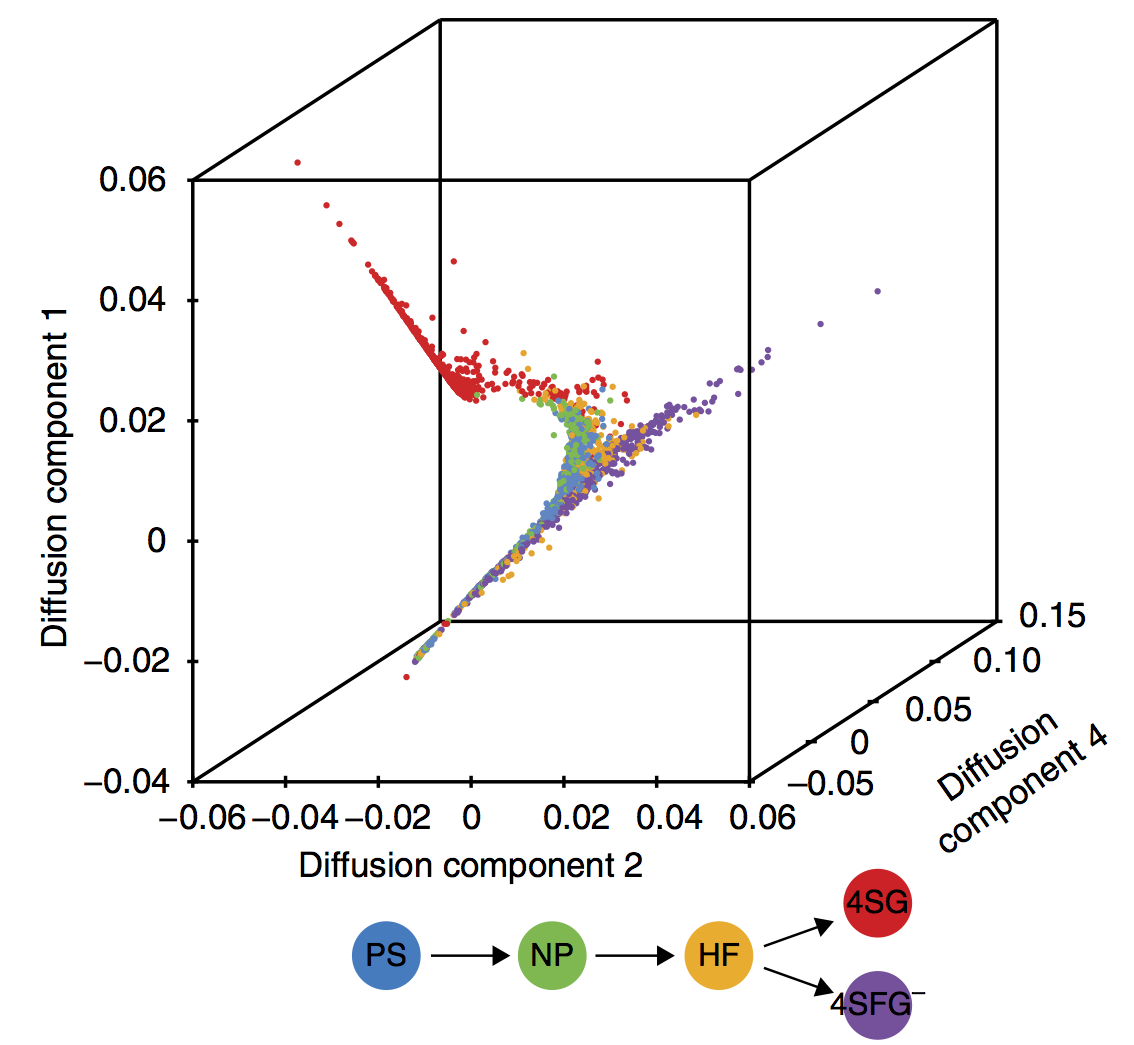
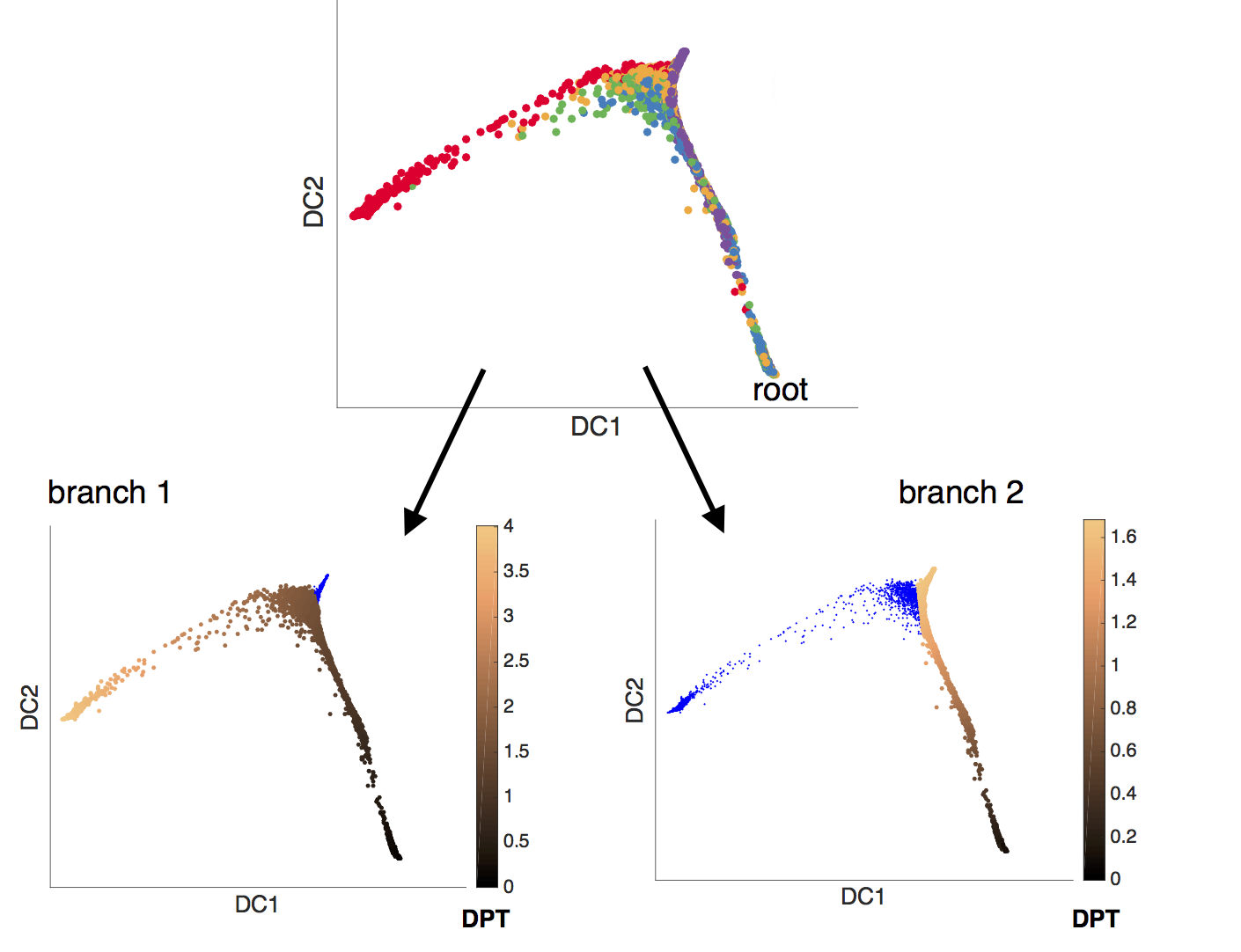
- branching pseudotime evolution of gene expression
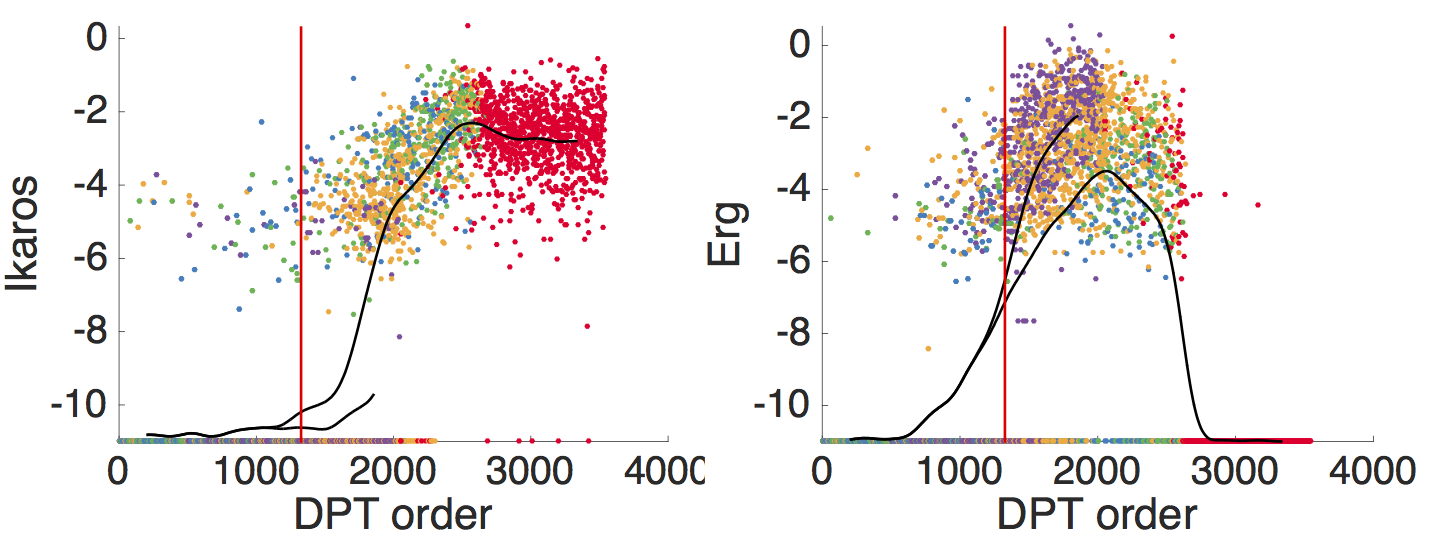
Gene expression data for branching lineages
- branching pseudotime evolution of gene expression

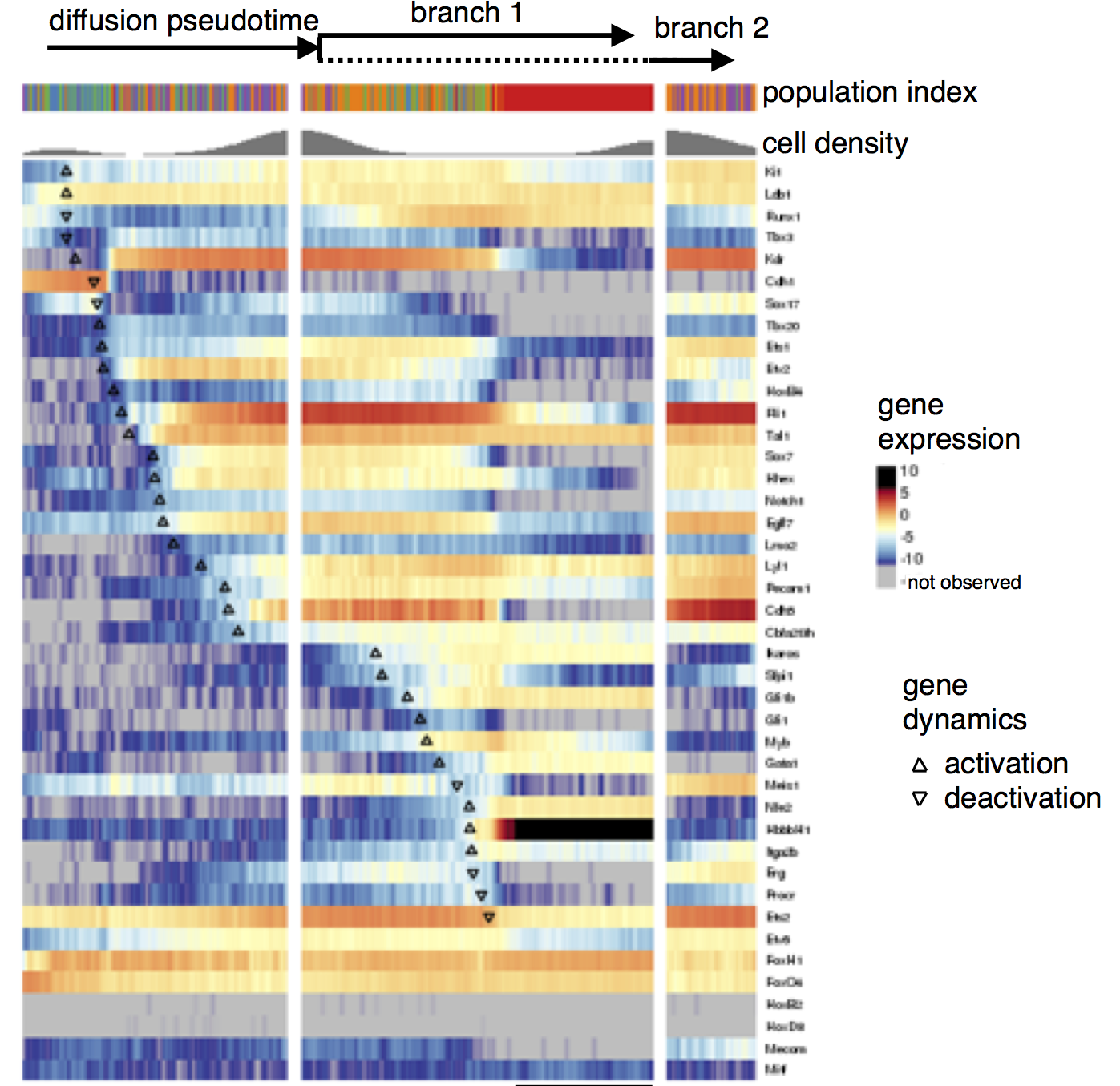
Gene expression data for branching lineages
- branching pseudotime evolution of gene expression
- here: ordered by switching time
▷ Learn about gene regulation?
- Gene that switches early and does not branch candidate for regulator?
- Gene that branches in different fates candidate for regulated gene?

(Causal) time series analysis
Model fitting
- ODE based model
Oconce, Haghverdi, Müller & Theis, Bioinformatics (2015) - Boolean network
Moignard, Woodhoouse ... Göttgens, Nat. Biotechn. (2015)
Granger Causality/Transfer Entropy
- Granger Causality ≃ Transfer Entropy
Barnett, Phys. Rev. Lett. (2009)
Causal Inference Methods
- PC algorithm
Spirtes et al. (2000) - Structural equation models
e.g. Peters, ..., Schölkopf, NIPS (2013)
Convergent Cross Mapping
- Taken's Theorem
Takens (1980)
Model fitting
- ODE based model
Oconce, Haghverdi, Müller & Theis, Bioinformatics (2015)
▷ edges using GENIE3, then optimize for ug(ˆx)
ddtˆxg=αug(ˆx)−λˆxg, p(D|θ)∝∏Tt=1exp(−(xtg−ˆxg(t,θ))22σ2) - Discrete state space model
Moignard, Woodhouse ... Goettgens, Nat. Biotech. (2015) - generate discrete state graph of 1-gene transitions
- check consistency of trial Boolean networks

(Causal) time series analysis
Model fitting
- ODE based model
Oconce, Haghverdi, Müller & Theis, Bioinformatics (2015) - Boolean network
Moignard, Woodhoouse ... Göttgens, Nat. Biotechn. (2015)
Granger Causality/Transfer Entropy
- Granger Causality ≃ Transfer Entropy
Barnett, Phys. Rev. Lett. (2009)
Causal Inference Methods
- PC algorithm
Spirtes et al. (2000) - Structural equation models
e.g. Peters, ..., Schölkopf, NIPS (2013)
Convergent Cross Mapping
- Taken's Theorem
Takens (1980)
Granger Causality / Causal Inference Methods
Conditional independence tests: Xti⊥⊥X(t−1)j|X(t−1)k1,X(t−1)k2,...
- Only works well if there is a high amount of dynamic information and no error in time variable. Both is not the case!
- Instead: time series with geometric constraints associated with branchings. Cannot be exploited by local independence tests.


(Causal) time series analysis
Model fitting
- ODE based model
Oconce, Haghverdi, Müller & Theis, Bioinformatics (2015) - Boolean network
Moignard, Woodhoouse ... Göttgens, Nat. Biotechn. (2015)
Granger Causality/Transfer Entropy
- Granger Causality ≃ Transfer Entropy
Barnett, Phys. Rev. Lett. (2009)
Causal Inference Methods
- PC algorithm
Spirtes et al. (2000) - Structural equation models
e.g. Peters, ..., Schölkopf, NIPS (2013)
Convergent Cross Mapping
- Taken's Theorem
Takens (1980)
Convergent Cross Mapping

Idea: Reconstruct regulating gene from the history of the regulated gene.
Convergent Cross Mapping
Idea: Reconstruct regulating gene from the history of the regulated gene.
▷ Can exploit branching geometry!
▷ But: no statistical formulation!


New method: statistical test for coupling functions
Rationale
Xtj=fj(X(t−1)j,X(t−1)i1,X(t−1)i2,...)⇔Fj(Xtj,X(t−1)j,X(t−1)i1,X(t−1)i2,...)=0Statistically test whether X(t−1)i1 contributes to Fj by testing for the existence of a function g g(Xtj,X(t−1)j,X(t−1)i2,...)=X(t−1)i1.
Implicit function theorem: if there is no g, Fj is constant w.r.t X(t−1)i1.
Definition of test: bivariate case
Consider Xtj=fj(X(t−1)j,X(t−1)i). How to statistically test for the existence of mapping the g:Xj→Xi?
zji=¯Δji−¯δi√(ˆσΔji)2/n+(ˆσδji)2/n where Δ(a)tji=1|N(a)tj|∑t′∈N(a)tjdtt′i is the variation across realizations for a fixed value in the domain Xj δ(a)ti=12(d(a)t(t−1)i+d(a)(t+1)ti) is the dynamic variation in the codomain.
Numerical experiment



Summary
- Goal: infer gene regulation from pseudotime order.
- Problem: very little dynamic information, traditional approaches fail, instead use branching geometry.
- Convergent Cross Mapping: can exploit branching geometry but serious flaws.
- New method: statistical test for coupling functions via implicit function theorem.